Sentiment Analysis using Naive Bayes Classifier

Implimenting Naive Bayes classifier from scratch for sentiment analysis of IMDB dataset

Saahil Anande

Last updated on Dec 1, 2021 9 min read blog

https://miro.medium.com/max/1200/1*ZW1icngckaSkivS0hXduIQ.jpeg

Switch to dark mode for better readability

Some outputs are shortened on the blog for easier reading. For Complete Jupyter Notebook click below.

Link to Jupyter Notebook

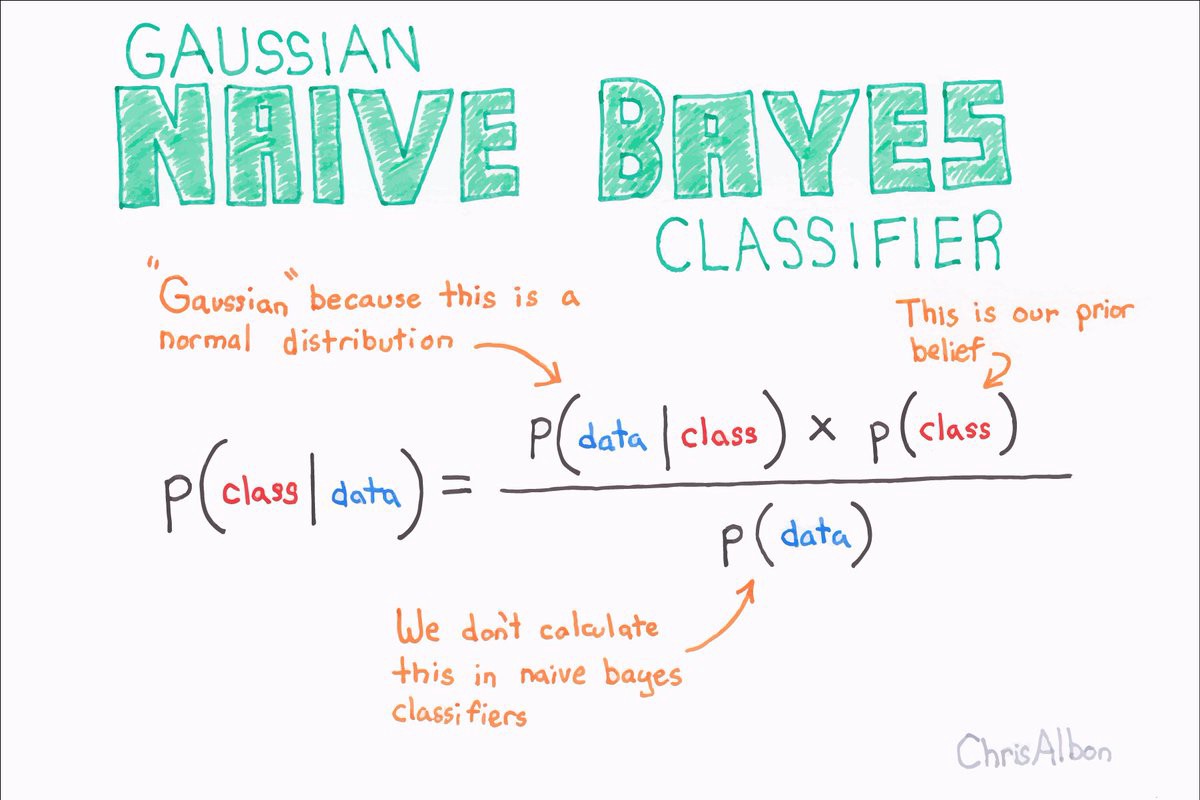
What is Bayes Theorem?

Bayes’ theorem is a way to figure out conditional probability. Conditional probability is the probability of an event happening, given that it has some relationship to one or more other events. For example, your probability of getting a parking space is connected to the time of day you park, where you park, and what conventions are going on at any time. Bayes’ theorem is slightly more nuanced. In a nutshell, it gives you the actual probability of an event given information about tests. Source

Below is the formula for conditional probability using Bayes Theorem:

Source

What is the relevance of each word in ‘Naive Bayes Classifier’?

It is a classification technique based on Bayes’ Theorem with an assumption of independence among predictors. In simple terms, a Naive Bayes classifier assumes that the presence of a particular feature in a class is unrelated to the presence of any other feature.

For example, a fruit may be considered to be an apple if it is red, round, and about 3 inches in diameter. Even if these features depend on each other or upon the existence of the other features, all of these properties independently contribute to the probability that this fruit is an apple and that is why it is known as ‘Naive’.Source

Naive: The word ‘Naive’ indicates that the algorithm assumes independence among attributes Xi when class is given:

P(X1, X2, …, Xd|Yj) = P(X1| Yj) P(X2| Yj)… P(Xd| Yj)

Bayes: This signifies the use of Bayes theorem to calculate conditional probablity

Classifier: Shows that the application of the algorithm is to classify a given set of inputs

Accuracy on test dataset before smoothening: 14%

Final accuracy on test dataset after performing laplacian smoothening: 81%

References at the end of the page

IMPORT REVIEW DATA

we take the IMDB dataset and import into our code. Here I stored the dataset in googledrive and we imported the dataset from there.

SPLITING THE DATA INTO TRAIN TEST VALIDATION

We first calculate how many sentences are present in the dataset and which belong to which data set. As we can see the data set is eqally divided into postive and negative review with total sentence 1000.

For training and testing we divid the dataset to test, train , validation sets.

Build a vocabulary as list.

Now to build vocabulary we split each sentence into words and count the frequency of each word.

review_list=[]
word_list=[]
word_list2 = []
word_list3 = []
positive_count=[]
negative_count = []
total_count= []
a=[]
from collections import Counter

review_list=train_review.values.tolist()


for i in range(len(train_review)):
  if review_list[i][1] == 1:
    for words in review_list[i][0].lower().split():
      words = words.replace(".","").replace("?","").replace("!","").replace(",","").replace("(","").replace(")","")
      word_list.append(words)
      positive_count = list(Counter(word_list).items())
      positive_count.sort(key=lambda x:x[1], reverse=True)


  if review_list[i][1] == 0:
    for wordsx in review_list[i][0].lower().split():
      wordsx = wordsx.replace(".","").replace("?","").replace("!","").replace(",","").replace("(","").replace(")","")
      word_list2.append(wordsx)
      negative_count = list(Counter(word_list2).items())
      negative_count.sort(key=lambda x:x[1], reverse=True)

  for wordss in review_list[i][0].lower().split():
    wordss = wordss.replace(".","").replace("?","").replace("!","").replace(",","").replace("(","").replace(")","")
    word_list3.append(wordss)
    total_count = list(Counter(word_list3).items())
    total_count.sort(key=lambda x:x[1], reverse=True)

omit rare words

Probability of the occurrence

P[“the”] = num of documents containing ‘the’ / num of all documents

To calculate the bayes theorem we need to calulate probability of each word to its respected document.

Conditional probability based on the sentiment

P[“the” | Positive] = # of positive documents containing “the” / num of all positive review documents

P[“the” | Negative] = # of positive documents containing “the” / num of all positive review documents

Total positive probability and negative probability

Sentiment ANALYSIS

Now since we are using the naive bayes approach we consider each words to be independent of each other and calculate the bayes theorem. Here we check if the word is present in the respected attribute, if its present we multiple the independent probability given class to those word who are also present in the attribute sentence and if the word is not present we consider the propability as zero and multiple it.

we compare the total multiplication of probability of each sentence and see which class probability is more then it belong to that class.

def sentiment(line):
  # for word in line[i][0].lower().split():
  pred = []
  mul_pos_prop = float(totalposprob)
  mul_neg_prop = float(totalnegprob)
  for word in line.lower().split():
    word = word.replace(".","").replace("?","").replace("!","").replace(",","").replace("(","").replace(")","")
    # if word not in [i[0] for i in omited_positive_count]:
    if word not in [i[0] for i in postive_prop]:
      # print("NOT IN POS",word)
      # print(word,"0","1")
      ll = [word,"0","1"]
      pred.append(ll)
    else:
      for props in postive_prop:
        if word == props[0]:
          # print(props[0],props[1],"1")
          ll = [props[0],props[1],"1"]
          pred.append(ll)

    # if word not in [i[0] for i in omited_negative_count]:
    if word not in [i[0] for i in negative_prop]:
      # print("NOT IN NEG",word)
      # print(word,"0","0")
      ll = [word,"0","0"]
      pred.append(ll)
    else:
      for prop in negative_prop:
        if word == prop[0]:
          # print(prop[0],prop[1],"0")
          ll = [prop[0],prop[1],"0"]
          pred.append(ll)
    
  for r in pred:
    if r[2] == '1':
      mul_pos_prop = mul_pos_prop*float(r[1])

    if r[2] == '0':
      mul_neg_prop = mul_neg_prop*float(r[1])

  if mul_neg_prop>mul_pos_prop:
    return 0
    # print(mul_neg_prop,"n")
    
  if mul_neg_prop<mul_pos_prop:
    return 1
    # print(mul_pos_prop,"p")

Calculate accuracy using dev dataset

SMOOTHING

What is Laplace Smoothing?

If one of the conditional probabilities is zero, then the entire expression becomes zero. To solve this error we use Lapace Smoothing. To perform Laplace smoothing we add 1 to the numerator and ‘v’ to the denomenator of all probabilites. where ‘v’ is the total number of attribute values that Xi can take. Here the attribute can take only 2 values of we add 1 in the numerator and add 2 in the denominator.

def Smoothing(line):
  pred = []
  mul_pos_prop = float(totalposprob)
  mul_neg_prop = float(totalnegprob)
  for word in line.lower().split():
    if word not in [i[0] for i in smooth_postive_prop]:
      ll = [word,1/(len(smooth_postive_prop)+2),"1"]
      pred.append(ll)
    else:
      for props in smooth_postive_prop:
        if word == props[0]:
          # print(props[0],props[1],"1")
          ll = [props[0],props[1],"1"]
          pred.append(ll)

    if word not in [i[0] for i in smooth_negative_prop]:
      # print("NOT IN NEG",word)
      # print(word,"0","0")
      ll = [word,1/(len(smooth_negative_prop)+2),"0"]
      pred.append(ll)
    else:
      for prop in smooth_negative_prop:
        if word == prop[0]:
          # print(prop[0],prop[1],"0")
          ll = [prop[0],prop[1],"0"]
          pred.append(ll)
    
  for r in pred:
    if r[2] == '1':
      mul_pos_prop = mul_pos_prop*float(r[1])

    else:
      mul_neg_prop = mul_neg_prop*float(r[1])

  if mul_neg_prop>mul_pos_prop:
    return 0
    # print(mul_neg_prop,"n")
    
  if mul_neg_prop<mul_pos_prop:
    return 1
    # print(mul_pos_prop,"p")

Calculate accuracy after smoothing

Here we can see that the accuracy significantly increased to 81% from 14%

perform 5 fold cross validation

Cross-validation is primarily used in applied machine learning to estimate the skill of a machine learning model on unseen data. That is, to use a limited sample in order to estimate how the model is expected to perform in general when used to make predictions on data not used during the training of the model.

1.Shuffle the dataset randomly. 2.Split the dataset into k groups 3.For each unique group:

1.Take the group as a hold out or test data set
2.Take the remaining groups as a training data set
3.Fit a model on the training set and evaluate it on the test set
4.Retain the evaluation score

Source

s1=[]
s2=[]
s3=[]
s4=[]
s5=[]
train_set=[]

s1 = train_review.iloc[:160].values.tolist()
s2 = train_review.iloc[160:320].values.tolist()
s3 = train_review.iloc[320:480].values.tolist()
s4 = train_review.iloc[480:640].values.tolist()
s5 = train_review.iloc[640:800].values.tolist()

firsttrain=[]
firstvalid=[]
for item in s1:
  firsttrain.append(item)
for item in s2:
  firsttrain.append(item)
for item in s3:
  firsttrain.append(item)
for item in s4:
  firsttrain.append(item)
for item in s5:
  firstvalid.append(item)


secoundtrain=[]
secoundvalid=[]
for item in s2:
  secoundtrain.append(item)
for item in s3:
  secoundtrain.append(item)
for item in s4:
  secoundtrain.append(item)
for item in s5:
  secoundtrain.append(item)
for item in s1:
  secoundvalid.append(item)

thirdtrain=[]
thirdvalid=[]
for item in s3:
  thirdtrain.append(item)
for item in s4:
  thirdtrain.append(item)
for item in s5:
  thirdtrain.append(item)
for item in s1:
  thirdtrain.append(item)
for item in s2:
  thirdvalid.append(item)


fourthtrain=[]
fourthvalid=[]
for item in s4:
  fourthtrain.append(item)
for item in s5:
  fourthtrain.append(item)
for item in s1:
  fourthtrain.append(item)
for item in s2:
  fourthtrain.append(item)
for item in s3:
  fourthvalid.append(item)

fifthtrain=[]
fifthvalid=[]
for item in s5:
  fifthtrain.append(item)
for item in s1:
  fifthtrain.append(item)
for item in s2:
  fifthtrain.append(item)
for item in s3:
  fifthtrain.append(item)
for item in s4:
  fifthvalid.append(item)


def fold(train):
  word_list=[]
  word_list2 = []
  word_list3 = []
  pp_count=[]
  nn_count = []
  tt_count= []

  for i in range(len(train)):
    if train[i][1] == 1:
      for words in train[i][0].lower().split():
        words = words.replace(".","").replace("?","").replace("!","").replace(",","").replace("(","").replace(")","")
        word_list.append(words)
        pp_count = list(Counter(word_list).items())
        pp_count.sort(key=lambda x:x[1], reverse=True)


    if train[i][1] == 0:
      for wordsx in train[i][0].lower().split():
        wordsx = wordsx.replace(".","").replace("?","").replace("!","").replace(",","").replace("(","").replace(")","")
        word_list2.append(wordsx)
        nn_count = list(Counter(word_list2).items())
        nn_count.sort(key=lambda x:x[1], reverse=True)

    for wordss in train[i][0].lower().split():
      wordss = wordss.replace(".","").replace("?","").replace("!","").replace(",","").replace("(","").replace(")","")
      word_list3.append(wordss)
      tt_count = list(Counter(word_list3).items())
      tt_count.sort(key=lambda x:x[1], reverse=True)

  return pp_count,nn_count,tt_count

pp_count1,nn_count1,tt_count1 = fold(firsttrain)
pp_count2,nn_count2,tt_count2 = fold(secoundtrain)
pp_count3,nn_count3,tt_count3 = fold(thirdtrain)
pp_count4,nn_count4,tt_count4 = fold(fourthtrain)
pp_count5,nn_count5,tt_count5 = fold(fifthtrain)


def prop(train,tc,pc,nc):
  tt_prob=[]
  for i in tc:
    eachprob =i[0],i[1]/len(train)
    tt_prob.append(eachprob)

  ppcount = 0
  npcount = 0
  for i in range(len(train)):
    if review_list[i][1] == 1:
      ppcount = ppcount + 1

    if review_list[i][1] == 0:
      npcount = npcount + 1

  pp_prop=[]
  for j in pc:
    eachposprob =j[0],j[1]/ppcount
    pp_prop.append(eachposprob)

  nn_prop=[]
  for i in nc:
    eachnegprob =i[0],i[1]/npcount
    nn_prop.append(eachnegprob)

  return tt_prob, pp_prop, nn_prop,ppcount,npcount

tt_prob1,pp_prop1,nn_prop1,ppcount1,npcount1 = prop(firsttrain,tt_count1,pp_count1,nn_count1)
tt_prob2,pp_prop2,nn_prop2,ppcount2,npcount2 = prop(secoundtrain,tt_count2,pp_count2,nn_count2)
tt_prob3,pp_prop3,nn_prop3,ppcount3,npcount3 = prop(thirdtrain,tt_count3,pp_count3,nn_count3)
tt_prob4,pp_prop4,nn_prop4,ppcount4,npcount4 = prop(fourthtrain,tt_count4,pp_count4,nn_count4)
tt_prob5,pp_prop5,nn_prop5,ppcount5,npcount5 = prop(fifthtrain,tt_count5,pp_count5,nn_count5)


def foldsentiment(line,pp_prop,nn_prop):
  # for word in line[i][0].lower().split():
  pred = []
  mul_pos_prop = 1
  mul_neg_prop = 1
  for word in line.lower().split():
    word = word.replace(".","").replace("?","").replace("!","").replace(",","").replace("(","").replace(")","")
    # if word not in [i[0] for i in omited_positive_count]:
    if word not in [i[0] for i in pp_prop]:
      # print("NOT IN POS",word)
      # print(word,"0","1")
      ll = [word,"0","1"]
      pred.append(ll)
    else:
      for props in pp_prop:
        if word == props[0]:
          # print(props[0],props[1],"1")
          ll = [props[0],props[1],"1"]
          pred.append(ll)

    # if word not in [i[0] for i in omited_negative_count]:
    if word not in [i[0] for i in nn_prop]:
      # print("NOT IN NEG",word)
      # print(word,"0","0")
      ll = [word,"0","0"]
      pred.append(ll)
    else:
      for prop in nn_prop:
        if word == prop[0]:
          # print(prop[0],prop[1],"0")
          ll = [prop[0],prop[1],"0"]
          pred.append(ll)
    
  for r in pred:
    if r[2] == '1':
      mul_pos_prop = mul_pos_prop*float(r[1])

    if r[2] == '0':
      mul_neg_prop = mul_neg_prop*float(r[1])

  if mul_neg_prop>mul_pos_prop:
    return 0
    # print(mul_neg_prop,"n")
    
  if mul_neg_prop<mul_pos_prop:
    return 1

    def foldaccuracy(dev,pp_prop,nn_prop):

  correct = 0

  for x in dev:
    result = foldsentiment(x[0],pp_prop,nn_prop)
    if result == x[1]:
      correct = correct + 1
  print("Accuracy is ",correct/len(dev)*100)
  gg = correct/len(dev)*100
  return gg


result1 = foldaccuracy(firstvalid,pp_prop1,nn_prop1)
result2 = foldaccuracy(secoundvalid,pp_prop2,nn_prop2)
result3 = foldaccuracy(thirdvalid,pp_prop3,nn_prop3)
result4 = foldaccuracy(fourthvalid,pp_prop4,nn_prop4)
result5 = foldaccuracy(fifthvalid,pp_prop5,nn_prop5)

meanresult= (result1 + result2 + result3 + result4 + result5)/5
print("accuracy of 5 fold cross validation without using smoothing is:",meanresult)

Top 10 words that predicts positive and negative class

P[Positive| word]

P[Negative| word]

Challenges faced:

Initialy I tried to implement smoothing I had trouble applying to IMDB dataset, I had to rewatch the lectures and understand the concept in depth to implement it. I was not able to implement the k-fold cross validation in much compact way which made the code repeatative and the computational time increase quite a bit because of this.

My Observations and Experiments:

I tried eleminating a few stop words from the data like ‘!’,'.','?','(',')',',' but this help me improve the accuracy of the classifier.

Before smoothing the probabilty that a single word is missing caused the whole sentence to became zero which was quite extreme and yield poor result. After smoothing the missing word became very small probability which significantly increased the accuracy.

Conclusion:

The final model accuracy on the test data is 81% The accuracy is pretty decent taking into consideration the naive assumption being made.I believe that, since the dataset had only 1000 inputs, the accuracy might have been lower. Having a larger dataset (more than 5000 sentences) could produce better results. In that case elemination of the stop words could also prove to be beneficial.